テーマ:アムダールの法則に基づいた、性能向上へ及ぼす影響

正解はこちら
解答:ウ
[基礎知識・用語のまとめ]
アムダールの法則・・・ある計算機システムとその対象とする計算についてのモデルにおいて、その計算機の並列度を上げた場合に、並列化できない部分の存在、特にその割合が「ボトルネック」となることを示した法則のことを言います。
全体としての性能向上比は次の式で表されます。

[解法]
並列化可能部分の割合をr(0≦r≦1)、プロセッサの数をn(n≧1)として、アムダールの関係式を表すと以下のようになります。
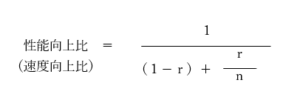
ここで、0≦r≦1なので、プロセッサnが十分大きくなると、分母の r/n はの値は、非常に小さく無視できるレベルになります。よって、速度向上比は 1 / (1-r) で近似できるようになってしまうため、速度向上比は、プロセッサを増やしてもこの近似値に漸化的に近づきます。
したがって、選択肢「ウ」が正解となります。
その他の選択肢については、以下の通りです。
ア→すべての計算処理が並列化できる場合、並列化可能部の割合rは1になります。このため、関係式は以下のようにあらわせるため、速度向上比は、プロセッサ数に比例して増加することがわかり、漸化的に近づくことはありません。
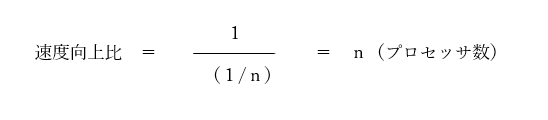
イ→例えば、r=0.5、n=2とすると、分母は0.5よりも大きくなり、速度向上比は2倍より小さくなるので、誤りということがわかります。
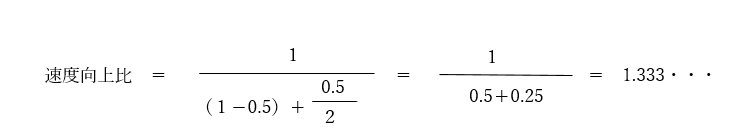
エ→並列化できる計算処理の割合が増え、プロセッサ数も増えれば、速度向上比は増加するが、減少することはないので、誤りです。
[参考]
プロセッサを4倍にしても、実際の速度は4倍にはならず(例えば1.6倍程度となり)、いくら増やしても、特定のスピード以上(例えば1.8倍以上)は早くならないということ、、、らしい
利用させていただきました素材へのリンク
うさちゃこちゃんねる様 https://www.youtube.com/channel/UCQcDdg4W6r5OfcB1JTcpABw




コメント