テーマ:排他的論理和の相補演算
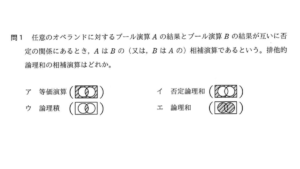
正解はこちら
解答:ア
[基礎知識・用語のまとめ]
オペラント・・・コンピュータの演算における値や変数のことです。 オぺランドは演算の種類や内容を表す演算子(オペレータ)によって演算対象となるもので、例えば「7×3」という計算式があれば、「7」と「3」がオペランドとなります。ただ、今回のケースでは、論理記号に関する話になりますので、具体的な例は出てきていません。
相補演算・・・集合演算の結果が互いに否定の関係になるものです。 つまり、Aとnot Aの関係や、A and Bとnot(A and B)といった否定の関係をいいます。

用語に関しての説明がややこしくしているけれど、単に「排他的論理和の相補演算はどれ?」という問題ね。
[解法]
演算Aの相補演算とは、演算Aの演算結果(真偽)と結果が否定関係、つまり、全く逆になる演算のことなので、演算Aの否定と等価(演算結果が同じ)になります。
二つのオペラント(演算対象)A、Bに対して、”・”(論理積)、”+”(論理和),” ̄”(論理否定)を用いて排他的論理はを表すと
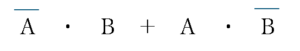
となり、これをベン図であらわすと、次のようになります。
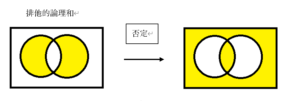
したがって正解は「ア」です。
[参考]
排他的論理和の否定を論理式で行う場合は、次のようになる、、、らしい。

利用させていただきました素材へのリンク
うさちゃこちゃんねる様 https://www.youtube.com/channel/UCQcDdg4W6r5OfcB1JTcpABw
ここまで読んでくれてありがとう!!

感謝!



コメント