テーマ:カルノー図と対等な論理式
正解はこちら
解答:エ
[この問題が言いたいことを一言でいうと]
カルノー図における論理式の表現(まとめ)を正しく行いなさい。
[基礎知識・用語のまとめ]
論理式・・・・値が1となるときの確定状態を記号で表現します。
カルノー図・・1953年に米ベル研究所のモーリス・カルノー (Maurice Karnaugh)がベイチ図 (Veitch diagram)の改良として考案した図法です→つまりカルノーは人名です。

[注目点]
・カルノー図におけるポイント
カルノー図は状態の簡略化を導き出すため、状態が共有されている順番で縦横に記載します。また、最上行と最下行、最右列と最左列はつながっていると解釈します。

[解法]
カルノー図の1が隣り合っている部分に注目します。
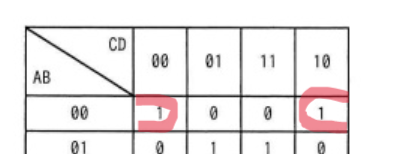
① 左上のマス(1)はA=0かつB=0かつC=0かつD=0の時1 と読めます。「かつ」という表現は積集合「・」であらわされ、0は否定記号(記号の上にバーをつける形)であらわされます。(Aの場合は¯A)
つまり、¯A・¯B・¯C・¯D=1と書きあらわすことができます。
同様に右上のマスは、¯A・¯B・C・¯D=1
ここで、1を求めたい場合、¯A・¯B・¯Dが確定していれば、Cが何であろうが1になりますよね?ということがわかります。
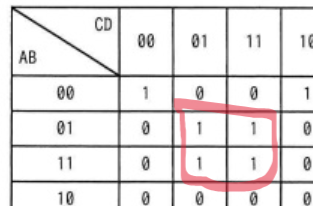

②①と同様に②の隣接部分も等式表現で確認します。中央4マスの式は以下の通り
(左上)¯A・B・¯C・D=1 (右上)¯A・B・C・D=1
(左下)A・B・¯C・D=1 (右下)A・B・C・D=1
つまり、B・Dがそろっていれば、AとCが何であろうと1になりますよね?となります。
つまり①と②をまとめると、¯A・¯B・¯DまたはB・Dがそろっていれば1になりますよね?となります。ここでまたはという表現は和集合「+」となりますので、結果的に「エ」である¯A・¯B・¯D+B・Dとなります。
[参考]
回路を組むにあたり、必要な素子の数(0、1を制御するために必要なスイッチの数)を減らせます。

利用させていただきました素材へのリンク
うさちゃこちゃんねる様 https://www.youtube.com/channel/UCQcDdg4W6r5OfcB1JTcpABw



コメント